Recommender systems have been around since the early ’90s. Since then, they became part of our lives, more than we are aware of.
Information filtering actually started receiving a lot of attention in the scientific community, and for a good reason…
They are incredibly practical and can make a significant contribution to the industry because they can help a user save a lot of time by searching through countless subjects just to pick one.
Table of Contents

Introduction to recommender systems
Recommender systems or recommendation systems are algorithms created to suggest similar, additional products/data to users or consumers. The AI uses Big Dada to fetch and recommend relevant products/data to users based on their past behaviours, preferences, and choices.
For example, Netflix uses a recommender system to suggest movies and shows to its customers based on the movies and shows they have already watched. Similarly, Amazon uses a recommender system to recommend products to its customers based on the products they have already purchased. TikTok, Instagram and Facebook use a recommendation engine to show personalized content to every user of their platform.
Depending on the user preferences, the AI continuously learns and AB tests strategies based on user behaviour.

The traditional recommender systems are ignoring the interactions between users and, from my point of view, that is a huge waste of potential.
There’s a saying — “birds of a feather flock together” and it is incredibly true when we are looking for something. A lot of times we ask our friends for recommendations — it does not matter if we are talking about books or movies, the concept stays.
The incorporation of social networks into a recommender system might make a major difference. There are some trust-based recommender systems, but their limitations are quite noticeable.
For example, they have weak generalization ability and impractical hypotheses, therefore they were outdated.
The integration of social networks would solve a lot of the problems that were present in their predecessors. Friendship among users will help us understand their ratings and by doing so, the interpretation of their preferences will be more accurate.
This is done by relying on a network graph and user-item matrix.
At the core, there will be users labelled — tags and the relationship between users. The matrix will be composed of user-item-tag and by clustering multiple users we can find out the similarity between them.
One important thing that must be taken into consideration is the difference in taste between friends because even though some people are sharing a connection, their tastes in certain areas might be different.

The Predecessors
Traditional Recommender Systems
These types of recommender systems can be divided into three major categories:
- Content-based filtering — this kind of filtering is based on tags, and it will recommend something to the user based on his previous choices therefore this system is incredibly limited. The recommendation accuracy will be horrible for a new user that has no history on the system, two items with the same tags, for the system would be indistinguishable and overall limited to tags that were in the past.
- Collaborative filtering — this system might be the most popular, so variations are present. The first approach would be memory-based and will search for unique items based on the opinion of similar users by finding the nearest neighbour from a rating matrix. The prediction is made based on the user’s history — different items that were rated for him. The other approach is model-based which uses a set of user ratings to learn a model that is used to make predictions. The problem with this approach is again the cold start and the fact that he will use ratings to make suggestions, meaning that a new product will require a lot of ratings from users for him to be suggested.
- Hybrid filtering — as the name suggests, this approach will mix a content-based filtering and collaborative filtering recommender system in diverse ways, depending on the situation and requirements.
Trust-based Recommender Systems
This type of system has reached its maturation and revolves around the fact that users are independent.
Again, there are a lot of variations — from one that uses a web of trust to generate the recommendations, to one that relies on a trust-aware approach using distrust metrics to improve the accuracy of models.
Since these types of systems were created by improving the traditional ones, they come in packages with the same disadvantages and weaknesses that need to be solved.
These are the systems we are most interested in because they promise to address and solve the weaknesses of their predecessors.
The model proposed is a probabilistic one that tries to integrate social information into the recommendation process, especially social connections.
The most recent approach is the one that treats friends who have different favours in diverse ways.
Firstly, the accuracy of the recommendation is improved by calculating the similarity between users based on the favours of each friend.
Secondly, they use a biclustering algorithm to search for “true” friends with similar favours to generate the final recommendation.
The integration of tags and “true” friends is used to analyze the social recommendation problem based on the matrix factorization framework.

The idea of integrating social networks into recommendation systems is incredible on its own so in the following sections, we are going to dive into the algorithm and workflow itself.

As we can see from Fig. 1, the two main steps are clustering the users to calculate similarities and obtain friendships and the other step is to model the framework by utilizing regulations.
In Fig. 2 we can see how a typical friends network graph looks. They represent 5 users — the nodes and 7 relationships (edges) between them. The rating from the users is either on a 5-point scale (5- best) or on tags expressing the level of favour of that item.

Fig. 3 Shows us the friendship matrix, 1 representing that there is a connection between users. The goal is to predict the missing value or tags from the user-item matrix.

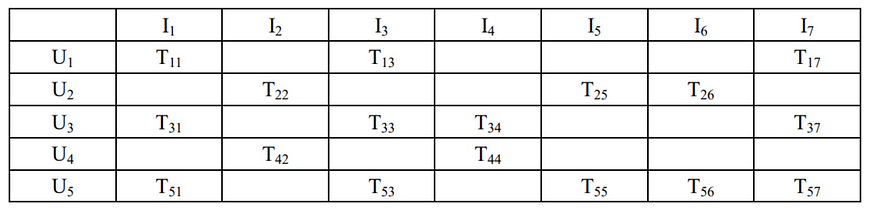
Based on the case described by the matrix from above we can see that the users U1 and U3 are sharing a connection also U1 and U2.
In the user-item matrix, we can see that U1 pays attention to I1, I3, I7, and U3 to I1, I3, and I4 but because he is friends with U1, the system will watch also I7 and U2 is watching I2, I5, and I6.
Because U1 and U3 share different interests, the system will recognize this similarity between tastes and recommend user1 I4 instead of recommending an item that is in U2’s sphere of interest.
The traditional recommender systems make recommendations based on a user-item matrix without considering the relationship between users and the systems that consider the relationship between users usually start from the assumption that users that have a connection will have similar tastes, but I am sure that everyone can agree that as friends we can have different tastes. Based on this, the algorithm proposes a matrix factorization framework with social recognition.
In the model described and as Fig. 1 shows, we must cluster users to obtain suitable groups of friends. The user item is translated into a double-dimensional matrix to keep the simplicity, but it can also be seen as a three-dimensional matrix, tags representing the third dimension.
Based on the items, we must classify the users into some stable groups and vice versa.
These new sets will create a stable matrix to prepare for clustering. The procedure runs until there are no new stable biclusters. The cluster-based algorithm used is the K-means algorithm.
After the algorithm finishes, we can calculate the similarity between users who share a friendship.
The similarity between users is based not only on “realistic” friendships but also on “personal” favours.
Let us say that user U1 is interested in I4 exactly like U4, but their tastes are completely different. The system will recommend that item only if U4 is an expert in that field.
The method of weight calculus in this model is by the formula

Where the weight of the tag t that was created by user U is equal to the sum of 1/(number of tags).
The “Mui” represents the list the user U gave to item I, meaning that a user may use multiple tags for the same item => the more tags the user gave to the item the smaller that tag’s weight will be.
This takes care of the scenario in which users add the same tag to multiple items.
The similarity between users is calculated by the fusion of biclusters with the corresponding tag. The case in which the friends are not in the same group is calculated differently.
One example is U1 is curious about I2 and even though U4 and U1 have different tastes the item I2 will be recommended only if U4 is an expert in that field. In order for that to happen there must be a similarity between the items that are in the U4’s sphere of interest.
The cold-start problem refers to the scenario in which a new user joins the network, and the recommender system will not know what recommendation to make or how to calculate the similarity between users.
But in this model when a user joins the network, he will pay attention to the existing users and those interactions will be seen as an initial friendship.
In this model, they map the user and item to the tag space and calculate the similarity based on the formula:
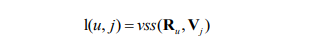
Where “Ru” is the tag vector of user u and “Vj” is the vector of item j. And the similarity is calculated using the same formula as the similarity between users.

The social regulation process consists of a matrix regulation framework where we define for each different recommendation task the most suitable group of friends and the approach chosen was individual-based.
But the integration is not only with the friendships among users but also with the item-user correlation.
In short, when we obtain the user and item biclusters and calculate the similarities between items and users in order to improve the prediction accuracy we also add the friend and item regularization.
Depending on the complexity of the relation to express, the model we build can be more or less complex, ranging from basic models (logistic/linear regression for classification/regression) to deep neural networks.

Experimental Results
For the experimental part, we compare our results with the Pop approach the traditional, collaborative filtering, and social regularization.

“P@i” symbolize the precision value when a user recommends, I item, and “R@5” the recall value for a user that recommends 5 items


Different Approach
The centre of the collaborative sifting calculation is to calculate the likeness.
The SNE strategy can superiorly assess the calculation on the off chance that beneath certain edge esteem there are fewer separated hubs but more little communities in its similitude systems. It incorporates the taking after necessities.
- A Certain Edge Esteem. Relative to the complete asset, these suggested assets are very few. Subsequently, when we assess a calculation, the PCN arrange () as it were ought to be considered. Nevertheless, to have a comprehensive investigation, the VSN organize () and the SCN arrange () ought to be considered together.
- Less Separated Hubs. The recommendation algorithm is based on likeness. The disconnected hub is not like several other hubs. In this case, the calculation cannot deliver a proposal for these confined hubs. Subsequently, a great calculation may deliver a similitude arranged with less disconnected hubs and more Non-disconnected ones.
- More Communities. Each community () speaks to a diverse intrigued of clients. The more the communities, the nitty gritty highlights can they reflect, which makes the prescribed comes about more in line with the user’s taste.
- Fewer Hubs within the Biggest Community. Within the biggest community, there are as well numerous hubs to reflect the user’s taste in detail. The hubs within the biggest community should be as few as conceivable. Taking under consideration the past focuses, conjointly considering these diverse systems with a distinctive number of hubs, the score of the closeness arrange assessment (SNE) is depicted by Fig. 9 where SS is the score work of likeness organize, is the edge, is the number of all hubs within the arrange, is the number of Non-confined hubs within the organize, is the number of communities, and is the number of hubs within the biggest community.

Conclusion
Social network sites are exploding and will evolve even more so it is only logical to start using the relationship between users and the friendship between them to make the recommendation process easier.
As we saw from the results, the incorporation of social network information was incredibly beneficial.
The model described employed both rating records and user friendships to predict the missing values in the user-item matrix.
Social network information comes in handy when we cluster the data set to obtain a group of friends with similar favours and to calculate the similarity between them.
Resources
- Adomavicius G, Tuzhilin A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(6): 734–749.
- Brusilovsky, Peter, and David N. Chin. Preface to the special issue on personalization in social web systems. User Modeling and User-Adapted Interaction, 2013, 23(2–3): 83–87.
- Jamali M and Ester M. A Matrix Factorization Technique with Trust Propagation for Recommendation in Social Networks. In Proceedings of the 4th ACM Conference on Recommender Systems, Barcelona, Spain, September 26–30, 2010: 135–142.
- Massa P and Avesani P. Trust-aware collaborative filtering for recommender systems. Lecture Notes in Computer Science, 2004(3290): 492–508.
- Ozsoy M G, Polat F. Trust based recommendation systems. In Proceedings of the 2013 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, ASONAM’13, Niagara, ON, Canada, August 25–29, 2013: 1267–1274.
- Recommender Systems Based On Social Network Zhoubao Sun Lixin Han Wenliang Huang Xueting Wang Xiaoqin Zeng Min Wang Hong Yan S0164–1212(14)00206–4
- Multiangle Social Network Recommendation Algorithms and Similarity Network Evaluation Jinyu Hu, Zhiwei Gao, and Weisen Pan
- https://doi.org/10.1155/2013/248084